Assignment 1

Probability, Linear Algebra, and Computational Programming

Instructions

Instructions for all assignments can be found here. Note: this assignment falls under collaboration Mode 2: Individual Assignment – Collaboration Permitted. Please refer to the syllabus for additional information. Please be sure to list the names of any students that you worked with on this assignment. Total points in the assignment add up to 90; an additional 10 points are allocated to professionalism and presentation quality.

Learning Objectives

The purpose of this assignment is to provide a refresher on fundamental concepts that we will use throughout this course and provide an opportunity to develop skills in any of the related skills that may be unfamiliar to you. Through the course of completing this assignment, you will…

• Refresh your knowledge of probability theory including properties of random variables, probability density functions, cumulative distribution functions, and key statistics such as mean and variance.
• Revisit common linear algebra and matrix operations and concepts such as matrix multiplication, inner and outer products, inverses, the Hadamard (element-wise) product, eigenvalues and eigenvectors, orthogonality, and symmetry.
• Practice numerical programming, core to machine learning, by applying it to scenarios of probabilistic modeling, linear algebra computations, loading and plotting data, and querying the data to answer relevant questions.

We will build on these concepts throughout the course, so use this assignment as a catalyst to deepen your knowledge and seek help with anything unfamiliar.

For references on the topics in this assignment, please check out the resources page on the course website for online materials such as books and courses to support your learning.

Note: don’t worry if you don’t understand everything in the references above - some of these books dive into significant minutia of each of these topics.

Exercise 1 - Probabilistic Reasoning

1.1. Probabilistic Reasoning I. You are handed three fair dice and roll them sequentially. What’s the probability of the sum of the dice is 10 after you’ve rolled the first die and it shows a 1?

1.2. Probabilistic Computation I. Simulate the scenario in 1.1 by creating 1 million synthetic rolls of the three dice. Determine what fraction of outcomes that had a “1” for the first die also had a sum of 10 across the three die.

1.3. Probabilistic Reasoning II. A test for a rare disease has a 95% chance of detecting the disease if a person has it (true positive rate) and a 3% chance of wrongly detecting it if a person does not have it (false positive rate). If 1 in 1,000 people actually have the disease, what is the probability that a randomly chosen person who tests positive actually has the disease?

1.4. Discrete Probability Theory. A discrete random variable \(X\) is distributed as follows (probability mass function):

\(P(X = x) = \begin{cases} 0.2 & x = -1 \\ 0.5 & x = 0 \\ 0.3 & x = 1 \end{cases}\)

What is the expected value, \(E_X[X]\) and variance, \(Var_X(X)\) of the random variable \(X\)?

Exercise 2 - Probability Distributions and Modeling

You’ve been asked to create a model of wait time for customers at Olivander’s Wand Shop. While they strive for the perfect match, there is some cleanup between customers that has been keeping wait times high. They’re open 8 hours a day and the maximum wait time is 8 hours (we won’t assume it’s possible not to be seen, assuming you’re willing to wait). Define the continuous random variable \(X = \{\text{wait time for service as a fraction of 8 hours}\}\) . This means that \(x=1\) represents a full day’s wait, or 8 hours, \(x=0.5\) represents half a day wait or 4 hours. Additionally, the valid values of \(X\) are between 0 and 1 (\(0\leq x \leq 1\)).

We’ll begin by analyzing some data of past visits to the shop to understand the customer wait time experience through our data (2.1-2.2). Then, we’ll select a model we hypothesize might fit our situation well and evaluate its properties like mean and variance (2.3-2.7). We’ll also evaluate the quality of the fit of the model as compare to our data (2.8-2.11). Lastly, we’ll explore how this approach can be used to generate insights (2.12).

Reviewing our wait time data

2.1. Load and plot a histogram of your wait time data. The file is wait_times.csv in the data/a1 folder here on Github. I recommend using the simple np.loadtxt() function to accomplish this so you can quickly load it in as a numpy array. Remember, the value 1 represents a full 8 hour work day so you should see your data are all in the range of \([0,1]\). Please use 10 bins and limit the bin edges to the range \([0,1]\) (no values should be plotted outside that range).

2.2. Mean, variance, and standard deviation of the data. Compute the mean, variance, and standard deviation of the wait time data. Report the mean and standard deviation in both the original units (in \([0,1]\)) and in hours (the variance is unitless).

Creating a model for the wait time distribution

Take a moment to review the distribution of the data. The most common distribution is normal, but this doesn’t seem normally distributed. Neither does it look uniform. The shape actually looks like it may be exponentially distributed, but truncated at 1. It’s not uncommon to have this type of shape in a wait time model, but this introduces a challenge since we can’t just use the standard exponential distribution since an exponential distribution is defined on a domain from 0 to infinity, but our data is defined between 0 and 1. Let’s create a customized distribution as a model for our data and see how well it represents the key statistics of our data.

In this section, please note the list of equations and identities at the end of this document as they may be useful for several questions.

2.3. Probability Density Functions (PDFs). Compute the value of \(\alpha\) that makes \(f_X(x)\) a valid probability density function:

\(f_X(x) = \begin{cases} \alpha e^{-x} & 0 \leq x \leq 1 \\ 0 & \text{else} \end{cases}\)

Provide this value exactly (with no approximation) and also provide and approximate decimal value with a precision to three decimal places.

2.4. Cumulative Distribution Functions (CDFs). Compute the cumulative distribution function (CDF) of \(X\), \(F_X(x)\), where \(F_X(x)=P(X<x)\) (here, \(P(\cdot)\) represents the probability of the event within the brackets). Be sure to indicate the value of the CDF for all values of \(x\in(-\infty,\infty)\). Express your CDF using the variable \(\alpha\) to provide the precise CDF.

2.5. Expected Value. Compute the expected value of \(X\), \(E_X[X]\). Provide this value exactly (no approximations and only in terms of \(e\) and \(\alpha\)) and provide a numerical approximation of the expected value to 3 decimal places. Also provide the approximate number of hours waiting (to 3 decimal places).

2.6. Variance and Standard Deviation. Compute the variance of \(X\), \(Var(X)\) approximately to 3 significant figures, meaning 3 digits without leading zeros (e.g. 12.3, 0.123, 0.00123, all have 3 significant figures). Using the variance, calculate the standard deviation and express this standard deviation in both the original units and units of hours.

2.7. Plotting your functions. Create functions to implement your PDF, \(f_X(x)\), and CDF, \(F_X(x)\), for all possible values of \(x\). Using these functions, plot the PDF and CDF on the inverval \(-0.5 \leq x \leq 1.5\).

Evaluating the quality of the model

2.8. Compare the empirical CDF to the modeled CDF. Plot both of these on the interval \(0 \leq x \leq 1\). For the empirical CDF of the data from wait_times.csv, you can plot the empirical CDF by sorting the data in ascending order, your \(x\) values, and assigning the \(y\) value as the cumulative fraction of samples that are smaller than or equal to each \(x\) value.

2.9. Calculate the inverse CDF to enable you to generate synthetic data. Create a numerical simulation of this process. Doing this for a custom PDF is easier than you may think. We typically have access to uniformly distributed samples (through np.random.rand), and we can transform these uniform samples into any distribution we wish. To do this, we can input uniform variates through the inverse of the CDF. If \(U\) is a uniformly distributed random variable and \(F_X(x)\) is the CDF of the distribution we’re looking to model, then \(F_X^{-1}(U)\) will be distributed in the same way as \(X\), as shown below in Figure 1.

Synthetic Data Generation

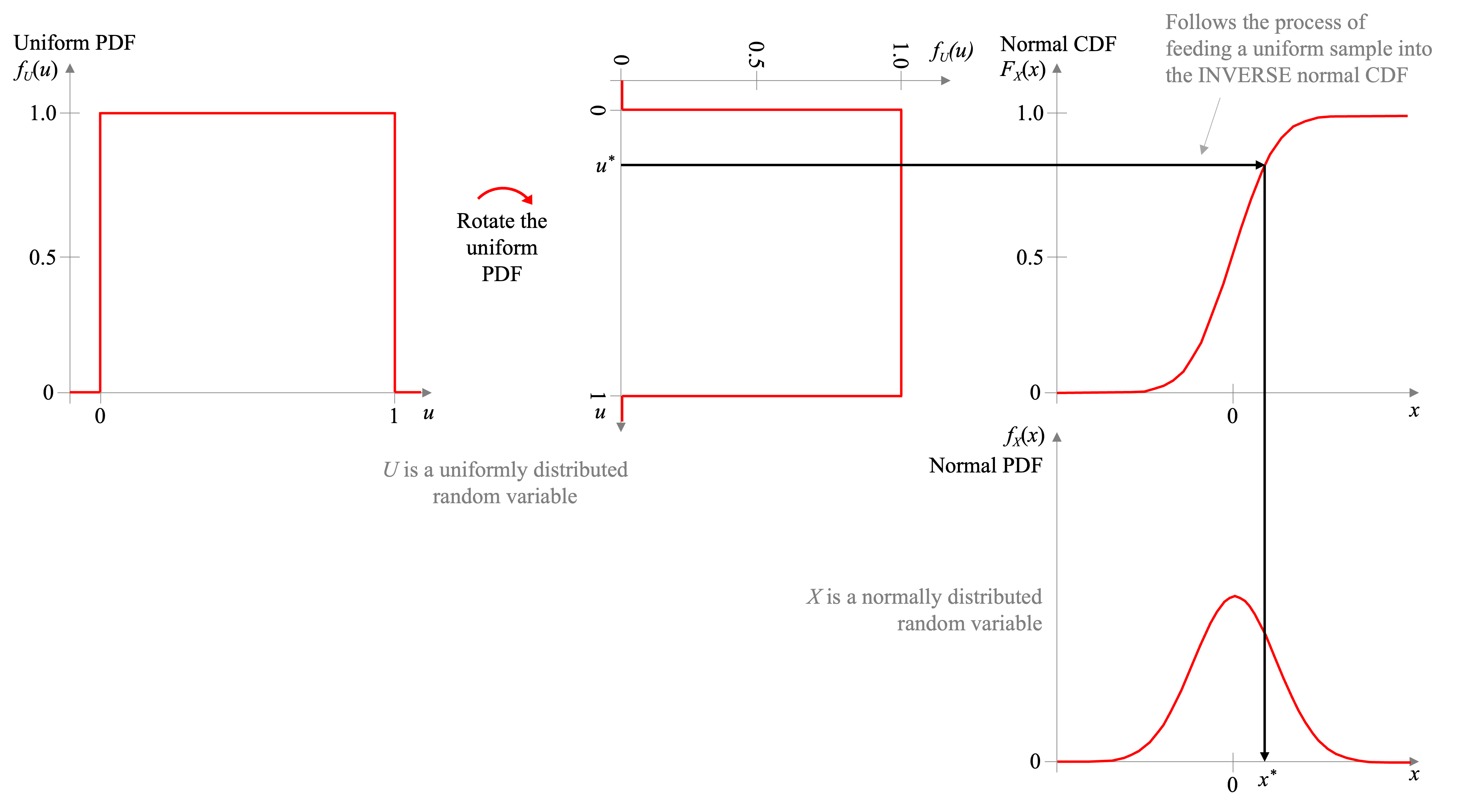
Figure 1. Demonstrating the process of transforming a uniformly distributed random variable into almost any distribution (here we transform into a normal). Here we show the transformation a sample, \(u^{\ast}\), from a uniform distribution to a sample, \(x^{\ast}\) from a normal distribution by applying the inverse of the CDF of \(X\) to \(u^{\ast}\), that is \(x^{\ast} = F_X^{-1}(u^{\ast})\).

Calculate the inverse of the CDF, \(F_X^{-1}(y)\) (We use the variable \(y\) as the input into this function to denote that we’re inputting the “output” of the CDF into this inverse CDF).

2.10. Generate synthetic data using the inverse CDF by transforming uniform samples. Once you have your inverse CDF, code it up and use it to create synthetic samples from the last step. To do so, first generate 10,000 samples from the uniform distribution and then feed those uniform variates through the inverse CDF to generate synthetic variates from our wait time model. Using those samples, compute the mean and standard deviation. Present the mean and standard deviation in a table comparing (a) the empirical values computed from wait_times.csv, your theoretical model values calculated earlier, and your computed values calculated from your synthetic model. How do they compare?

2.11. Run a statistical test to evaluate the goodness of fit of your model to the empirical data from wait_times.csv. To evaluate the goodness of fit of the model to the data, one tool is the Kolmogorov–Smirnov test, or simply the KS test. The two-sample version of this test evaluates the maximum distance between two CDFs, each calculated from samples of data. In this case, the null hypothesis states that the samples are drawn from the same distribution. We can conclude that the sample data are well-represented by the reference distribution if we do NOT reject the null hypothesis. If we test at the 5% significant level, then we can conclude that data come from the same distribution if the p-value is greater than 0.05 (we fail to reject the null hypothesis).

Compare the sample of data from wait_times.csv to the synthetic sample from the model distribution and run the KS test. Also compare the sample data to the uniform distributed data you generated before transforming it into the synthetic samples. For the test use scipy.stats.kstest.

Using the model to understand wait times

2.12. Computing probabilities. Having a way of generating synthetic data can allow us to easily compute probabilities. Compute the probabilities of the following events using the synthetic data samples that you generated.

1. Wait time is more than 6 hours
2. Wait time is less than 1 hour
3. Wait time is less than one additional hour given the client has already been waiting for 3 hours (i.e., the probability of the wait time being less than 4 hours if they have already waited for 3 hours)
4. Wait time is between 3 and 5 hours
5. What is the 90th percentile of wait times?
6. What is the 99th percentile of wait times?

Exercise 3 - Linear Algebra Operations and Theory

3.1. Matrix manipulations and multiplication. Machine learning involves working with many matrices and understanding what their products represent, so this exercise will provide you with the opportunity to practice those skills.

Let \(\mathbf{A} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\), \(\mathbf{b} = \begin{bmatrix} -1 \\ 1 \end{bmatrix}\), \(\mathbf{c} = \begin{bmatrix} 1 \\ 2 \end{bmatrix}\)

Compute the following by hand or indicate that it cannot be computed. For any cases where an operation is invalid and cannot be computed, explain why it is invalid.

1. \(\mathbf{A}\mathbf{A}\)
2. \(\mathbf{A}\mathbf{A}^{\top}\)
3. \(\mathbf{A}\mathbf{b}\)
4. \(\mathbf{A}\mathbf{b}^{\top}\)
5. \(\mathbf{b}\mathbf{A}\)
6. \(\mathbf{b}^{\top}\mathbf{A}\)
7. \(\mathbf{b}\mathbf{b}\)
8. \(\mathbf{b}^{\top}\mathbf{b}\)
9. \(\mathbf{b}\mathbf{b}^{\top}\)
10. \(\mathbf{A}\circ\mathbf{A}\)
11. \(\mathbf{b}\circ\mathbf{c}\)
12. \(\mathbf{b}^{\top}\mathbf{b}^{\top}\)
13. \(\mathbf{b} + \mathbf{c}^{\top}\)
14. \(\mathbf{A}^{-1}\mathbf{b}\)
15. \(\mathbf{b}^{{\top}}\mathbf{A}\mathbf{b}\)
16. \(\mathbf{b}\mathbf{A}\mathbf{b}^{{\top}}\)

Note: The element-wise (or Hadamard) product is the product of each element in one matrix with the corresponding element in another matrix, and is represented by the symbol “\(\circ\)”.

3.2. Matrix manipulations and multiplication using Python. Repeat 3.1, but this time using Python. If you are using a vector, make sure the dimensions of the vector match what you’d expect, for example, matrix \(\mathbf{b}\) is a \([2 \times 1]\) vector. In NumPy, unless you’re specify, you’ll like create a one-dimensional array of length 2 rather than a \([2 \times 1]\) vector if you don’t specify - be careful of this potential pitfall. Refer to NumPy’s tools for handling matrices. There may be circumstances when Python will produce an output, but based on the dimensions of the matrices involved, the linear algebra operation is not possible. Note these cases and explain why they occur. Please provide both the Python code AND the output of that code showing your result. If the output is an error, comment out the code and note that it cannot be computed.

Be sure to use the right operator for each operation: Matrix multiplication: @; Element-wise multication: *. For this exercise, only use one of those to operators for matrix or vector multiplication.

3.3. Vector Norms. Norms are the effective lengths of vectors. For example, the Euclidean norm, or \(L_2\) norm (denoted as \(||\mathbf{\cdot}||_2\)), is the most common of several types of norms. The \(L_2\) norm can be calculated for a vector \[\mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}\] as follows: \[||\mathbf{x}||_2 = \sqrt{\displaystyle \sum_{k=1}^n x_k^2} = \sqrt{\mathbf{x}^{\top}\mathbf{x}}\]

What is the \(L_2\) norm of vectors \(\mathbf{d}_1 = \begin{bmatrix} 2^{-1/2} \\ -2^{-1/2} \\ 0 \end{bmatrix}\) and \(\mathbf{d}_2 = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}\)?

3.4. Orthogonality and unit vectors. Orthogonal vectors are frequently used in machine learning in topics such as Principal Components Analysis and feature engineering for creating decorrelated features. Knowing what an orthogonal or orthonomal basis is for a space is an important concept. Find all values of unit vectors, \(\mathbf{d}_3\), that complete an orthonormal basis in a three-dimensional Euclidean space along with the two vectors: \(\mathbf{d}_1 = \begin{bmatrix} 2^{-1/2} \\ -2^{-1/2} \\ 0 \end{bmatrix}\) and \(\mathbf{d}_2 = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}\).

For review, vector \(\mathbf{x}_1\) is orthonormal to vector \(\mathbf{x}_2\) if (a) \(\mathbf{x}_1\) is orthogonal to vector \(\mathbf{x}_2\) AND \(\mathbf{x}_1\) is a unit vector. Orthogonal vectors are perpendicular, which implies that their inner product is zero. A unit vector is of length 1 (meaning its \(L_2\) norm is 1).

3.5. Eigenvectors and eigenvalues. Eigenvectors and eigenvalues are useful for numerous machine learning algorithms, but the concepts take time to solidly grasp. They are used extensively in machine learning including in Principal Components Analysis (PCA) and clustering algorithms. For an intuitive review of these concepts, explore this interactive website at Setosa.io. Also, the series of linear algebra videos by Grant Sanderson of 3Brown1Blue are excellent and can be viewed on youtube here. For these questions, numpy may once again be helpful.

1. In Python, calculate the eigenvalues and corresponding eigenvectors of matrix \(\mathbf{B}= \begin{bmatrix} 1 & 2 & 3 \\ 2 & 4 & 5 \\ 3 & 5 & 6 \end{bmatrix}\)
2. Choose one of the eigenvector/eigenvalue pairs, \(\mathbf{v}\) and \(\lambda\), and show that \(\mathbf{B} \mathbf{v} = \lambda \mathbf{v}\). This relationship extends to higher orders: \(\mathbf{B} \mathbf{B} \mathbf{v} = \lambda^2 \mathbf{v}\)
3. Show that the eigenvectors are orthogonal to one another (e.g. their inner product is zero - just compute the inner product and show it is approximately 0). This is true for eigenvectors from real, symmetric matrices. In three dimensions or less, this means that the eigenvectors are perpendicular to each other. Typically we use the orthogonal basis of our standard x, y, and z, Cartesian coordinates, which allows us, if we combine them linearly, to represent any point in a 3D space. But any three orthogonal vectors can do the same. This property is used, for example, in PCA to identify the dimensions of greatest variation.

Exercise 4 - Numerical Programming with Data

Loading data and gathering insights from a real dataset. In data science, we often need to have a sense of the idiosyncrasies of the data, how they relate to the questions we are trying to answer, and to use that information to help us to determine what approach, such as machine learning, we may need to apply to achieve our goal. This exercise provides practice in exploring a dataset and answering question that might arise from applications related to the data.

Your objective. For this dataset, your goal is to answer the questions below about electricity generation in the United States.

Data. The data for this problem can be found in the data\a1\ subfolder in the notebooks folder on github. The filename is egrid2016.xlsx. This dataset is the Environmental Protection Agency’s (EPA) Emissions & Generation Resource Integrated Database (eGRID) containing information about all power plants in the United States, the amount of generation they produce, what fuel they use, the location of the plant, and many more quantities. We’ll be using a subset of those data.

The fields we’ll be using include:

field	description
SEQPLT16	eGRID2016 Plant file sequence number (the index)
PSTATABB	Plant state abbreviation
PNAME	Plant name
LAT	Plant latitude
LON	Plant longitude
PLPRMFL	Plant primary fuel
CAPFAC	Plant capacity factor
NAMEPCAP	Plant nameplate capacity (Megawatts MW)
PLNGENAN	Plant annual net generation (Megawatt-hours MWh)
PLCO2EQA	Plant annual CO2 equivalent emissions (tons)

For more details on the data, you can refer to the eGrid technical documents. For example, you may want to review page 51 and the section “Plant Primary Fuel (PLPRMFL)”, which gives the full names of the fuel types including WND for wind, NG for natural gas, BIT for Bituminous coal, etc.

There also are a couple of “gotchas” to watch out for with this dataset:

• The headers are on the second row and you’ll want to ignore the first row (they’re more detailed descriptions of the headers).
• NaN values represent blanks in the data. These will appear regularly in real-world data, so getting experience working with these sorts of missing values will be important.

Questions to answer:

4.1. Which power plant generated the most energy in 2016 (measured in MWh)?

4.2. Which power plant produced the most CO2 emissions (measured in tons)?

4.3. What is the primary fuel of the plant with the most CO2 emissions?

4.4. What is the name of the northern-most power plant in the United States?

4.5. What is the state where the northern-most power plant in the United States is located?

4.6. Plot a bar plot showing the amount of energy produced by each fuel type across all plants.

4.7. From the plot in (D), which fuel for generation produces the most energy (MWh) in the United States?

4.8. Which state has the largest number of hydroelectric plants? In this case, each power plant counts once so regardless of how large the power plant is, we want to determine which state has the most of them. Note the primary fuel for hydroelectric plants is listed as water in the documentation.

4.9. Which state has generated the most energy (MWh) using coal? You may also want to explore the documentation for the isin() method for pandas. Note: in the eGrid documentation, there are multiple types of coal listed; be sure to factor in each type of coal.

4.10. Which primary fuel produced the most CO2 emissions in the United States? We would like to compare natural gas, coal, oil, and renewables but the current categories are much more specific than that. As a first step, group the data as shown below, replacing the existing labels with the replacements suggested. For example, BIT and LIG should be replaced with COAL.

• COAL = BIT, LIG, RC, SUB, WC
• OIL = DFO, JF, KER, RFO, WO
• GAS = BFG, COG, LFG, NG, OG, PG, PRG
• RENEW = GEO, SUN, WAT, WDL, WDS, WND

You may want to create a function that does this replacement prior to running your code. You can check whether or not it was successful by verifying that each of the values that should be replaced has been replaced - check that before moving on with the question.

You will want to use ‘PLCO2EQA’ to answer this question as it’s the quantity of emissions each plant generates.

Appendix: Definitions and identities

The symbology in this assignment conforms to the following convention:

Symbol Example	Meaning	Possible variations
\(X\)	A random variable	Upper case, non-bolded letter
\(\bar{X}\)	The complement of a random variable	Upper case, non-bolded letter with bar
\(\mathbf{x}\)	Vector (\(N \times 1\))	Lower case, bolded letters/symbols
\(\mathbf{X}\)	Matrix (\(N \times M\))	Upper case, bolded letters/symbols
\(P(\cdot)\)	Probability of the event within the parenthesis	Parenthesis may include one event or more events
\(A \cap B\)	Intersection of \(A\) and \(B\), that is the case of events \(A\) and \(B\) occurring simultaneously	Two random variables represented by upper case unbolded letters

Below is a list of potentially helpful identities and equations for reference.

Identities and equations	Description
\(E_X[X] = \displaystyle \int_{-\infty}^{\infty} x f_X(x) dx\)	Expected value of continuous random variable \(X\)
\(Var_X(X) = E_X[X^2]-E_X[X]^2\)	Variance of random variable \(X\)
\(\sigma_X(X) = \sqrt{Var_X(X)}\)	Standard deviation of \(X\) as a function of variance
\(\displaystyle P( X \vert Y)= \frac{P(X \cap Y)}{P(Y)}\)	Conditional probability of event \(X\) given event \(Y\) has occurred
\(\displaystyle P(Y \vert X)= \frac{P(X \vert Y)P(Y)}{P(X)}\)	Bayes’ Rule
\(\displaystyle F_X(x) = \int_{-\infty}^{x} f_X(x) dx\)	CDF as a function of PDF
\(\displaystyle f_X(x) = \frac{dF_X(x)}{dx}\)	PDF as a function of CDF
\(P(X \leq x) = F_X(x)\)	Probabilistic definition of the CDF
\(P(a < X \leq b) = F_X(b) - F_X(a)\)	Probability the \(X\) lies between \(a\) and \(b\)
\(P(A) + P(\bar{A}) = 1\)	The sum of the probability of an event and its complement is 1
\(\displaystyle P(Y) = P(Y \vert X)P(X) + P(Y \vert \bar{X})P(\bar{X})\)	Law of Total Probability
\(\displaystyle \int e^{-x} dx = -e^{-x}\)	Indefinite integral
\(\displaystyle \int x e^{-x} dx = -e^{-x}(x+1)\)	Indefinite integral
\(\displaystyle \int x^2 e^{-x} dx = -e^{-x}(x^2+2x+2)\)	Indefinite integral
\(\displaystyle \begin{bmatrix} a & b \\ c & d \end{bmatrix}^{-1} = \frac{1}{ad-cb} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}\)	\(2 \times 2\) matrix inversion formula